Conocimientos de perspectiva básica
| Arte | Ciencias | Turismo | Gastronomía | Pasiones | Glosarios |
Conocimientos de perspectiva básica | |||||||
| |||||||
| | |||||||
Dividir en profundidad un espacio en partes iguales | |||||
| Dividir en profundidad un espacio en partes iguales en el plano horizontal a partir de las diagonales. Cuando tenemos que dibujar edificios, caminos, vías, suelos de baldosas, postes y árboles en hilera, etc. hemos de construir un cuadriculado que nos permita colocar a cada cosa en su sitio y del tamaño adecuado. Esto exige una técnica a seguir en el trazado y que podemos resolver de dos maneras: usando diagonales y otra usando un segundo punto de fuga. 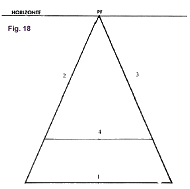 Supongamos que queremos dibujar una línea férrea que se pierde en el horizonte, pareciendo que las dos vías se juntan en un punto sobre la línea del horizonte, cuando la razón nos dice que los raíles, por ser paralelos, nunca llegan a encontrarse. Desde un punto de fuga situado sobre la línea del horizonte, trazaremos dos líneas, que serán las vías, y que en el dibujo están marcadas con los números 2 y 3, y sigamos suponiendo que estamos situados en el centro de la vía. Fig. 18. 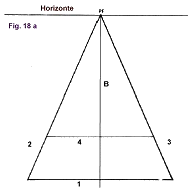 Lo primero que haremos es definir y marcar la longitud de la primera traviesa (1), que siempre será paralela a la línea del horizonte, y los dos raíles (2 y 3) que se pierden en el horizonte, dando la sensación que se juntan en un vértice que será el punto de fuga (PF). La segunda traviesa
(4), hemos de posicionarla a ojo, es decir, observando la posición relativa
en proporción a la longitud, para hacernos idea de la distancia, por supuesto
paralela a la línea del horizonte y por lo tanto a la traviesa (1). Una
vez ubicada la segunda traviesa (4), tracemos una mediana a la traviesa
o línea (1), con lo que quedará dividido el cuadrilátero inicial en dos.
Fig. 18 a. 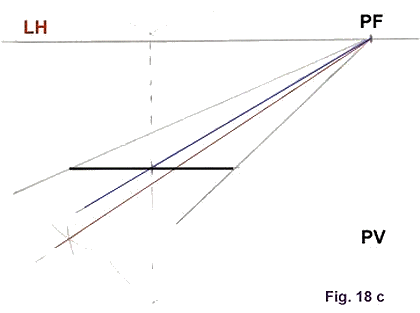
Lo que tenemos que hacer es dividir la primera traviesa en partes iguales, por
lo que NO tendremos que trazar una bisectriz sino una mediana desde el punto medio
de la primera traviesa, siendo esta, uno de los lados del triángulo escaleno.
Recordemos la definición de mediana:" es la línea que une cualquier vértice con
el punto medio del lado opuesto al vértice". (Ver figura 18 c) La línea en rojo
es la bisectriz, la línea en azul es la mediana. Ahora trazamos una diagonal a uno de los cuadriláteros, prolongándola hasta cortar al lado 2 en el punto b y, desde este punto, trazamos una paralela a la "traviesa" anterior obteniendo así, la posición de la tercera "traviesa". Repitiendo la operación "n"; veces obtendremos las siguientes posiciones. Puntos c, d, e, . n, hasta obtener el esquema definitivo o que consideremos. | |||||

Búsqueda personalizada
|
| Inicio de Sección |
| Portada |
| Esta página forma parte de: todaCultura.com | Copyright © todaCultura | Condiciones de uso | Utilidades Webmaster | Privacidad |