Entre todo el saber que almacenaron se halla el conocimiento del número mágico Phi, (la divina proporción) que luego aplicarían en construcciones tanto de tipo civil como religioso. Phi, el número sagrado o de oro, no debe entenderse como un número sino como una relación de proporciones. Es la base de la proporción armónica que está presente en muchos de los órdenes de nuestra vida, la naturaleza, las relaciones entre las frecuencias de las notas musicales, . ha representado para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino . por cierto el que puso nombre a este número, fue el matemático alemán Martín Ohm denominándole Phi en honor a Fidias (Phidias) el escultor griego, que tanto y tanto usó.

Pero el que lo dio a conocer al gran publico fue el fraile italiano Lucca Pacioli cuando en 1497, escribió y publicó un libro tituldo: "De divina Proportione", donde se revelaba, por fin, el secreto de la belleza, que en realidad se basaba en lo que los escolares actuales conocen como "regla de tres". Pacioli se inspiraba en las ideas de Piero della Francesca, un hombre que hoy conocemos a través de su obra pictórica, pero que en su tiempo era más conocido por ser el autor de "De Abaco", un manual de matemática para comerciantes.

Remontémonos al VI a.C, Pitágoras huye de la Isla de Samos perseguido por Polícrates y se establece en Crotona (Italia) y funda la sociedad Pitagórica, una escuela filosófica que trataba de explicar la vida mediante números, cuyo principio básico era: "todo en número", cuya contraseña secreta era una estrella de cinco puntas, que se obtiene trazando las diagonales de un pentágono regular y curiosamente, si dividimos cualquiera de sus diagonales por el valor de uno de sus lados obtendremos el número mágico 1,61803, como veremos a continuación.

El pentágono y las relaciones con el número Phi.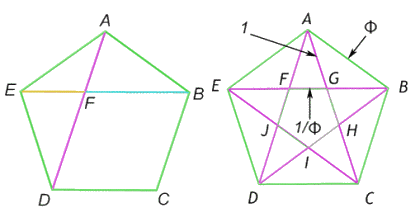

En el primer pentágono ABCDE, trazo una diagonal AD y otra BE que se cruzan en F, si BF es igual a 1, BE es igual a Phi (Φ). En el segundo pentágono ABCDE, trazamos todas las diagonales con lo cual obtenemos una estrella de cinco puntas y otro pentágono FGHIJ. Si AG es igual a 1, AB es igual a Phi y FG al inverso de Phi: 1/F, es decir 0,618.
Si dividimos cualquiera de sus diagonales, por el valor de uno de sus lados, obtendremos el número mágico 1,61803.

El rectángulo áureo de Euclides.

A partir del cuadrado ABCD, Euclides obtiene el rectángulo áureo AEFD.

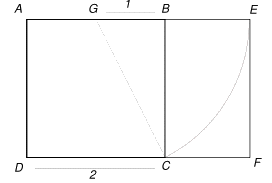
El rectángulo BEFC, es proporcional al rectángulo AEFD es asimismo áureo.
El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo.
Euclides en su proposición 2.11 de "Los elementos" obtiene su construcción. Partimos del cuadrado ABCD de lado 2, siendo G el punto medio de uno de sus lados. Por lo tanto tenemo las siguientes medidas:
GB = 1; BC = 2    y   GC = h

De acuerdo con el teorema de Pitágoras:

   h² = C² + C² por lo que,   GC² = BG² + BC² 

y resolviendo la ecuación obtenemos

. Volviendo a la figura del cuadrado ABCD, haciendo centro en G, punto medio de AB se obtiene el punto E y por lo tanto

resultando evidente que

concluyendo con el resultado

Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que éste último es asimismo un rectángulo áureo.

Phi a partir de un Segmento.

Enunciado: El numero Phi es una proporción de tal manera que se dividimos un segmento cualquiera en dos partes, a y b, la razón entre la totalidad del segmento y la parte a sea igual a la razón entre la parte a y la parte b.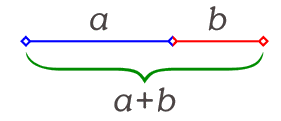

Expresado matemáticamente representaríamos esta proporción mediante la siguiente razón:

A esta razón, que cumple la propiedad, se le denomina razón áurea o número dorado. Podemos obtener este número a partir de la expresión anterior, despejando a utilizando la fórmula general de las ecuaciones de segundo grado, teniendo en cuenta que a > 0 : Dividiendo todo por b obtenemos:

a / b = 1,618 o lo que es lo mismo
b = a/1,618, expresado de otra forma
b = 1/1,618 . a;
b = 0,618 . a;
b/a = 0,618;
(a + b) 0,618 = a resolviendo que a +b = a / 0,618 y por lo tanto
(a + b) / a = 1 / 0,618; en definitiva (a + b) / a = 1,618, sustituyendo el número por sus valor volvemos al planteamiento inicial :

con lo que queda demostrado dicho planteamiento.

Phi en la sucesión de Fibonacci.
Se puede hallar este número también con la sucesión de Fibonacci. Esta sucesión matemática es la siguiente:

1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - 89 - 144 - 233...
Esta serie numérica, consiste en sumar el número anterior al número actual para obtener el siguiente, por ejemplo el siguiente a 5 es 5+3=8, ó el siguiente a 21 sería 21 + 13 = 34, pero cabría preguntarnos
¿qué tiene que ver esta sucesión con el número áureo?
Observad la siguiente tabla:

Comprobamos que a medida que avanzamos en la serie, las diferencias son cíclicas, cada vez más pequeñas acercándonos cada vez más al número Phi, siendo las aproximaciones una vez por exceso y la siguiente por defecto. De todo lo cual concluimos que, es una serie infinita cada vez más próxima al número Phi ... resultando en definitiva un logaritmo.

Phi en el triángulo de Pascal.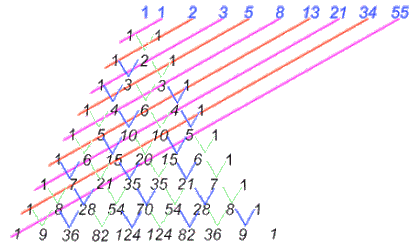

Este es el triángulo de Pascal que se forma, situando el número uno en los lados laterales del triángulo y los demás números, se hallan sumando los dos números situados en la línea superior del número en cuestión siguiendo la bifurcación en V según nos muestra el l dibujo.
Sumando los números situados en las diagonales, líneas rojas y moradas del dibujo, se obtiene la famosa sucesión de Fibonacci.

Referente al número áureo (Φ) hay más ...pero lo dejaremos para otro momento. No obstante, antes de terminar, hemos de advertir que, todo lo aquí expuesto no sirve de nada si a la hora de la práctica no sabemos aplicarlo y para ello existen una serie de útiles, trucos, recursos que conocen algunos profesionales y artistas, aunque ninguno de ellos nos muestra su forma de hacer. Entre todos los recursos existentes hay dos o tres cuyo conocimiento debe ser imprescindible, por ejemplo el patrón o patrones del número mágico y la sección áurea, el analizador de color que no es otra cosa que una tarjeta de color blanco con una pequeña ventana para visualizar y comparar los colores determinando el tono, pero sobre todos los recursos que podemos mencionar, destaca, lo que algún genio, nombró como la Máquina de la Perspectiva, de la cual prometo hablar, describir y forma de aplicación en los siguientes apartados:

• Recursos.
• Composiciones frecuentes.
• Máquina de la perspectiva.
• Visores aureos. Construcción